SITESWAP NOTATION DLA ZUPEŁNIE NIEZORIENTOWANYCH
Ostrzeżenie:
- Niniejsze opracowanie nie ma zamiaru pretendować do miana wyczerpującego, ani nawet zrozumałego,
- może zawierać mniej lub bardziej poważne błędy merytoryczne,
- autor nie odpowiada za żadne urazy (szczególnie ortopedyczne, ale i innej natury, np. epilepsja, zatwardzenie itd.) doznane podczas prób wykorzystania świeżo nabytej wiedzy w praktyce.
Na wstępie proponuję zaopatrzyć się w oprogramowanie, dzięki któremu będzie łatwo testować, wizualizować i przeprowadzać eksperymenty związane z żonglowaniem. Moimi faworytami są:
JoePass - dostępny pod adresem http://www.koelnvention.de/software/ - freeware działający pod Windows i na Mac'ach,
Jongl - dostępny pod http://www.jongl.de/ - freeware, Windows, Linux (pod linuksem zawsze wyzsza wersja dodatkowo zaopatrzona w generator J2)
J2 - najlepszy dostępny generator patternów, zawarty np. w programie Jongl (Linux)
Aby zrozumieć na czym polego notacja "siteswap" (czekam na propozycje tłumaczenia) posłużymy się kilkoma przykładmi, które mam nadzieję będą w stanie przybliżyć sprawę.
Przykład 1
 Kaskada z trzech piłek.
Kaskada z trzech piłek.
Opis sytuacji:
Piłki są naprzemiennie przerzucane z jednej do drugiej ręki w równych interwałach czasowych.
Następna piłka jest wyrzucana z przeciwnej ręki, gdy lecąca osiągnie najwyższy punkt lotu (a ściślej zaczyna spadać).
Jak łatwo zauważyć, ręce pracują w przeciwfazie. Wyobraź sobie teraz, że jest to robione w rytm tykającego metronomu. Przy każdym jego uderzeniu wykonywany jest jeden rzut, raz z prawej, raz z lewej ręki. Każda piłka jest wyrzucana w powietrze co trzecie tyknięcie metronomu (co trzeci beat) i wszystkie rzuty są takie same (wysokość). Z punktu widzenia notacji interesują nas tylko wyrzuty piłek. Obrazuje to rysunek poniżej.
Diagram
Oznaczenia na diagramie:
L/R - wyrzut lewą/prawą ręką piłki koloru strzałki,
początek strzałki oznacza moment wyrzutu, koniec lądowanie,
cyfry - ilość jednostek czasowych przez które piłka znajduje się w powietrzu,
oczywiście na osi umieszczono upływ czasu; jednostką jest tu jeden "beat",
kolory symbolizują kolory piłek, w tym przypadku RGB :-)
Przykład 2

Fontanna z czterech piłek.
Tak jak w kaskadzie z trzech piłek wyrzucamy piłki raz z lewej, raz z prawej ręki. Różnica polega na tym, że piłki lądują w tej samej ręce, z której zostały wyrzucone. Przyjmijmy, że robimy to w tym samym rytmie (metronom) co przy trzech piłkach. Wprowadza to konieczność rzucania piłek odpowiednio wyżej. Tutaj każda piłka rzucana jest co 4 jednostki czasu.
Teraz przyszedł czas na wytłumaczenie samej notacji:
każdy "pattern" opisny jest liczbami
liczby oznaczają jak w danym momencie ręka, na którą przyszła kolej wyrzuca piłkę
średnia arytmetyczna wyciągnięta z wszystkich liczb w patternie daje nam zawsze liczbę obiektów. Nie oznacza to jednak, że dowolny ciąg liczb spełniający warunek podzielności swej sumy przez liczbę całkowitą (liczba piłek) da nam w rezultacie prawidłowy siteswap
liczba 0 oznacza, że ręka w tym ruchu pozostaje pusta (ruch jałowy, lub brak ruchu - jak kto woli)
liczba 1 - szybkie przekazanie piłki z ręki do ręki (rzut po niskim łuku lub podanie)
liczba 2 - piłka jest trzymana w ręku i tak pozostaje do czasu, gdy w kolejnym ruchu tej ręki znajdzie się wyrzut
liczba 3 - przerzut z ręki do ręki na wysokości kaskady z trzech piłek
liczba 4 - podrzut na wysokości fontanny z czterech piłek
każda następna nieparzysta - przerzut z ręki do ręki na odpowiednio większej wysokości
każda parzysta - j.w. tylko piłka ląduje w tej samej ręce (por. z liczbą 4)
dla prostoty zapisu powyżej 9 stosuje się zamiast cyfr litery: 10 - a, 11 - b, 12 - c, ... Chodzi o to, że liczby zapisuje się bezpośrednio po sobie, bez odstępów, więc ciężko byłoby zinterpretować taki np. ciąg 10 (czy to 10, czy 1, 0 ?)
Wprowadzone powyżej zasady można zobrazować prostymi przykładami:
Kaskada z trzech piłek - zapis 33333..., w skrócie 3
Fonanna z czterech piłek - 4444..., czyli 4
Kaskada z pięciu piłek - 5555..., 5
Itd. do 9
... kaskada z 10 piłek - aaaa..., a
Przykład 3
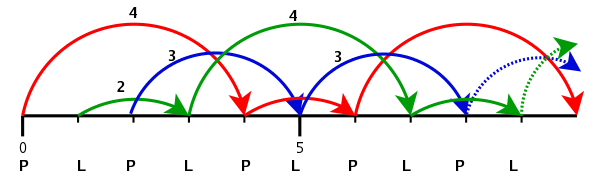
Dotąd było łatwo, więc trochę pokomplikujemy. Patterny nie muszą się przecież składać się z tych samych liczb. Zanalizujmy sobie łatwiutki układ na trzy piłki - 423. Najpierw wyrzucamy jedną piłkę pionowo, jak przy 4 piłkach, następnie drugą (z drugiej ręki) przerzucamy, jak przy 3 piłkach, a trzecią tak jak pierwszą. I tak w kółko. Wygląda to tak, jakbyśmy przerzucali jedną piłkę z ręki do ręki, a dwie pozostałe podrzucali aby opróżnić ręce na czas potrzebny do złapania i przerucenia piłki, która krąży. Każda piłka ma tutaj przyporządkowaną swoją sekwencję, która się powtarza. Dwie piłki rzucamy w rytmie 42 (w przeciwfazie) a trzecią cały czas 3.
Przykład 4
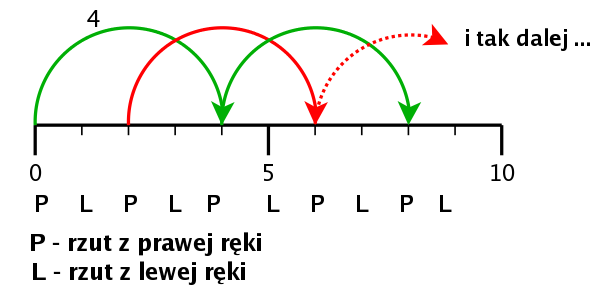
Jak zapisać rucanie dwoma piłkami w jednej ręce? Otóż trzeba sobie uzmysłowić, że jedna ręka nie robi nic, więc dla niej zawsze będzie 0. Druga ręka jest zapracowana, jak przy 4 piłkach, dla niej w świetle wszystkiego, co do tej pory wyjaśniono odpowiednią będzie liczba 4. Zapisać to można jako 40. Oczywiście cztery, zero, nie czterdzieści.
Przykład 5
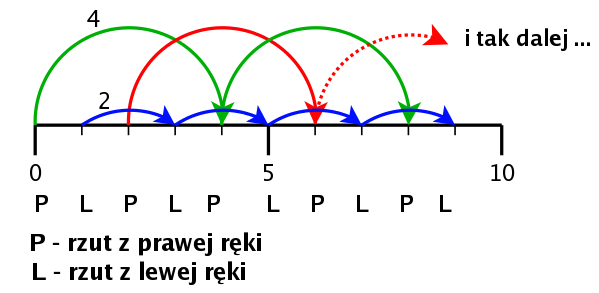
Jak zapisać rzucanie dwoma piłkami w jednej ręce podczas gdy w drugiej trzymamy jedną piłkę? Wystarczy zamienić zero z poprzedniego przykładu na dwa, które jak wiemy oznacza trzymanie piłki.
Zagadki
Jak opisać trzymanie piłki w jednej ręce, gdy druga jest pusta?
Jak zapisać trzymanie po jednej piłce w obu rękach?
To powinno wyjaśnić wszystko, jeśli chodzi o zapis asynchroniczny dla dwóch rąk, pod warunkiem, że nie chcemy łapać bądź wyrzucać więcej niż jedną piłkę jedną ręką. Wyrzut, w którym chcemy się pozbyć więcej niż jednej piłki z ręki nazywa się rzutem multipleksowanym (multiplexing). Rzut multipleksowy notuje się w nawiasie kwadratowym. Metoda ta pozwala na nauczenie się kilku patentów z większą ilością piłek niż jesteśmy w stanie rzucać pojedynczo (np. umiałem dosyć średnio rzucać czterema piłkami, a multipleksowałem już sześcioma). Rozróżnia się kilka typów rzutów tego rodzaju:
obie piłki wyrzucone na tę samą wysokość, jedna wraca do ręki rzucającej, jedna do ręki przeciwległej
piłki wyrzucone na różną wysokość wracają do tej samej ręki
j.w. tylko przerzut z ręki do ręki
piłki na różnych wysokościach, lecąca wyżej przerzut, lecąca niżej podrzut
j.w., tylko odwrotnie
Technicznie różnie jest z trudnością tych rzutów, są one tym trudniejsze im większa jest róznica pomiędzy poszczególnymi rzutami, np.:
[54] - jest stosunkowo łatwy
[75] - też nietrudny
[94] - teoretyzuję, ale pewnie trudny cholernie
[x1] - gdzie x to dowolna liczba, praktycznie niewykonalne
W tej klasie rzutów 2 nie musi oznaczać trzymania piłki, może to być równie dobrze rzut.
Przykłady:
24[45] - to jest tak zwany "Gatto multiplex", bardzo fajny patent
25[65]2
25[75]51
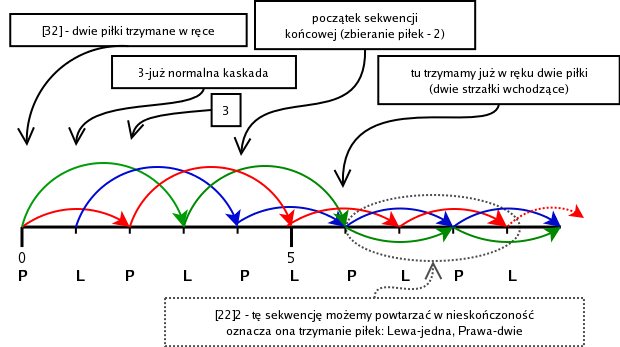
Skoro znamy już notację multiplexów spróbujmy zapisać w postaci siteswap'u start do kaskady z trzech piłek. Na początku trzymamy w jednej ręce dwie piłki, w drugiej jedną. Pierwszy rzut pochodzi z ręki, która trzyma dwie piłki, wyrzucana jest jedna (druga na razie pozostaje w ręce). No więc mamy [32] - teraz przechodzimy już do zwykłej kaskady ... 33333 ..... a jak zakończyć? Nie będziemy przecież rzucać w nieskończoność. [32]333...22[22] i już. Reausunując, sekwencja wygląda następująco: [32]33322[22], w tym 3 oraz końcowe 2[22] można powtarzać dowolną ilość razy.
Ręce mogą też pracować synchronicznie, czyli obie wyrzucać piłki w tym samym momencie. W zapisie rozwiązuje się to w ten sposób, że każdy moment czasowy notuje się w nawiasach
a o tym, czy rzut jest krzyżowy (crossing) decyduje obecność x przy liczbie.
Przykłady:
(4x,2x)
(6x,2x)
(6,6)(6,2)
(6,4)
(6x,2x)(2x,6x)
Można łączyć multipleksowanie z pracą synchronczną, np.:
([62],2) (6x,[22]) (2,[62]) ([22],6x)
Odpowiedzi do zagadek
20
22
Autor opracowania: Piniu - Tomasz Pichliński.
Inne artykuły:
- kaskada 3 piłkami
- fontanna 4 piłkami
- kaskada 5 piłkami